Spoiler
This is a LONG post. I realize that many of you may not wish to read it all.
Please refrain from voting "no" or "other" unless you post an intelligent counter argument. I spent a lot of time on this so the least you can do is make an informed decision and explain why you believe it to be the best option. I welcome any counter arguments as an intelligent discussion will help us (and PGI) improve the state of the game, something you obviously want if you are in this section of the forums.
"I don't like it" or "Its fine the way it is" are NOT counter arguments. They are opinions. It is my opinion that this is the best option for the game and so I have backed it with a detailed argument. It is your responsibility to back your claim with an argument as well.
If you do not read or understand everything and still vote no without a counter argument you are being useless. You have plenty of opportunities to be useless in life. Please give everyone the courtesy of not doing it here.
As I write this I realize that the weapon values are about to change and will change again in the future. I will not update the graphs as the point I am making is about the concept and model of exponential heat decay (real life physics/engineering) and how it will work in comparison to the current linear heat decay model in MWO. I can and may add more examples if you need me to.
With Honor,
Dem
This is a LONG post. I realize that many of you may not wish to read it all.
Please refrain from voting "no" or "other" unless you post an intelligent counter argument. I spent a lot of time on this so the least you can do is make an informed decision and explain why you believe it to be the best option. I welcome any counter arguments as an intelligent discussion will help us (and PGI) improve the state of the game, something you obviously want if you are in this section of the forums.
"I don't like it" or "Its fine the way it is" are NOT counter arguments. They are opinions. It is my opinion that this is the best option for the game and so I have backed it with a detailed argument. It is your responsibility to back your claim with an argument as well.
If you do not read or understand everything and still vote no without a counter argument you are being useless. You have plenty of opportunities to be useless in life. Please give everyone the courtesy of not doing it here.
As I write this I realize that the weapon values are about to change and will change again in the future. I will not update the graphs as the point I am making is about the concept and model of exponential heat decay (real life physics/engineering) and how it will work in comparison to the current linear heat decay model in MWO. I can and may add more examples if you need me to.
With Honor,
Dem
----
HEAT BALANCE
I think we can all agree that the current model for heat balance in MWO leaves something to be desired. We have seen multiple balance changes and tweaks that deviate further and further from what we once considered to be 'canon'. 1.4 Double Heat Sinks, Ghost Heat, and all the extreme heat balance tweaks may have all been unnecessary and can even be eliminated.
This model improves heat dissipation at higher levels with the heat transfer rate slowing as the heat approaches thermal equilibrium. The maximum heat level is equivalent to the number of effective heat sinks, encouraging heat neutral builds and making stock canon builds more viable. At the same time, this reduces the gap between single and true double heat sinks by making each more effective with respect to the heat generated, not the arbitrary 10 second turn.
Heat management is still a very important factor to this system. Sure, most cases and under some conditions this will be different from MWO but the heat system is different and that is to be expected. This is not a magical "keep everything in game the same but still fix the heat system" fix. Those don't exist. It is a "make heat more realistic and closer to lore" solution. Builds designed for a different heat system will behave differently but hopefully not too much. At the very least this proposal should be considered and tested in the public test server.
Don't forget there actually is a calculator included in all this, so please try it out.
The simple version:
Spoiler
This proposal aims to balance gameplay, encourage more heat neutral builds, and simulate real physics better than the current heat system in MWO.
In real life physics a high heat source like a cutting torch will transfer heat across a solid object much quicker than a low heat source like a candle. At the same time a hotter object will cool faster than a warm object. In MWO a hotter object will cool at the same speed as a warm object.
In real life, to calculate how hot two heat sources will make an object you simply add their heat. In MWO, a third imaginary heat is applied to this calculation.
The heat you generate from firing your weapons will go away faster the hotter you are. As your heat level approaches zero, the mech cools slower and slower. This means that when you chain fire a lot of low heat weapons your heat will balance out at a certain temperature. It also means that if you alpha strike or are really hot your mech will cool down pretty quickly at first and then start to level out.
The max heat level should be equal to the number of heat sinks you have, each single heat sink counting as 1 and each double counting as 2. This will prevent anyone from firing too many weapons at the same time because you will overheat very quickly. However, because you also cool down quickly you can fire some more weapons without having to wait a long time.
Additionally, firing low heat weapons will make your heat rise to however hot those weapons are because of the math used to calculate your heat level. In MWO your heat will constantly decrease to zero at a certain rate, so if you fire something that gives you 1 heat it will never show up on your heat scale.
This proposal aims to balance gameplay, encourage more heat neutral builds, and simulate real physics better than the current heat system in MWO.
In real life physics a high heat source like a cutting torch will transfer heat across a solid object much quicker than a low heat source like a candle. At the same time a hotter object will cool faster than a warm object. In MWO a hotter object will cool at the same speed as a warm object.
In real life, to calculate how hot two heat sources will make an object you simply add their heat. In MWO, a third imaginary heat is applied to this calculation.
The heat you generate from firing your weapons will go away faster the hotter you are. As your heat level approaches zero, the mech cools slower and slower. This means that when you chain fire a lot of low heat weapons your heat will balance out at a certain temperature. It also means that if you alpha strike or are really hot your mech will cool down pretty quickly at first and then start to level out.
The max heat level should be equal to the number of heat sinks you have, each single heat sink counting as 1 and each double counting as 2. This will prevent anyone from firing too many weapons at the same time because you will overheat very quickly. However, because you also cool down quickly you can fire some more weapons without having to wait a long time.
Additionally, firing low heat weapons will make your heat rise to however hot those weapons are because of the math used to calculate your heat level. In MWO your heat will constantly decrease to zero at a certain rate, so if you fire something that gives you 1 heat it will never show up on your heat scale.
Spoiler
Ghost Heat - we all know what this does. It adds large heat penalties to some weapons of certain types fired within a half second. This is never the case in real life and the need of ghost heat has been the subject of many arguments since its inception.
Ghost Heat - we all know what this does. It adds large heat penalties to some weapons of certain types fired within a half second. This is never the case in real life and the need of ghost heat has been the subject of many arguments since its inception.
Before people jump in saying how it fixed 6 PPCs stalkers or more "LOL You just want 4 PPCs again LOL!" I would like to remind people of all the reasons Ghost Heat is the single worst game design element ever committed to a game:
- Absolutely no UI. No indicators as to Ghost Heat limitations, when it kicks in, how much it has kicked in, etc. are given to players outside of that small hardcore handful of us that read the forums and/or spend time in Smurfy's. This is while they try to appeal to a casual demographic, no less.
- Rewards Macros and External Programs. Due to reason #1, the half-second timer isn't even indicated to the player so they know when it is safe to fire again. Thus most good players running boated weapons turn to macros to time it for them, while more casual players lose damage by trying to count it in their head, risking firing too early and cooking themselves.
- Many weapons nerf'ed that weren't problems. 9 MedLas? Not a problem. 4 Large Lasers? Not a problem. 4 AC/2? Not worth noting. Yet, these were all implemented hard and fast and have not been tweaked once.
- Completely illogical linking. 1x LRM20 3x LRM10 = 4x LRM20 Ghost Heat for 50 missiles. 2x LRM20 2x LRM5 = 0 Ghost Heat for 50 missiles. The list continues. Should ER Large and Large Pulse really be linked together?
- It's massively overly complicated. I know where the limits start and learned all the bizarre linkage rules, like how LRM5s are exempt, Streaks don't count towards a limit, how LPL and ER Large share a pool, etc. But then we get to the actual heat calculation which.. God help you. All most of us deal with is "Over X = Bad." But there is no rhyme, reason, or clarity at any given time as to why some ghost heat is so much worse than others, without complicated charts from the developer (that made things even worse) and large tables of numbers that actually at least show us some results (3rd party fanbase).
- Most of all, it didn't really work. What ultimately killed the PPC boat was fixing the XML data file for the PPCs. 4 PPC Stalkers - which were far better than 6 - continued until the day that happened, as did the general PPC Meta. There was a sharp drop in boat builds after Ghost Heat arrived but almost all of them were by people who didn't understand the rules for it and overcompensated with horrible builds. Twin AC/20 builds remain popular and pinpoint damage wasn't impacted in the slightest, just different weapons were used for it.
LINEAR DECAY
Spoiler
The current MWO heat model is a linear equation based purely on the number of heat sinks with a multiplier for map heat level. The best example of how this works is here. As best as I can tell the function operates the same today. The equation is simply
where
Effective Heat Sinks (EHS) is the total value of heat sinks, not necessarily the actual number of heat sinks. 20 Single Heat Sinks is 22 EHS. 20 Double Heat Sinks in the current game would be 20*1.4=28 EHS.
This means that heat will bleed at 0.1 Heat per Second, per Heat Sink.
Using this formula, there is a very large disconnect between the time to sink all heat with 10 heat sinks and 22 Double (1.4) heat sinks, let alone 22 true DHS (2.0). Using the above formula, 40 heat with 10 SHS will take 40 seconds to sink all heat. With 22 DHS (1.4) and at the max heat of 60.8, it will take about 24 seconds to drain the heat. If these were 22 DHS (2.0), the max heat would be 74 and it would take about 17 seconds to cool. If this were the case, one could fire 4 ERPPCs every 13 seconds and be heat neutral. Obviously this is too many PPCs at once way too often when a Mech with 10 single heat sinks can fire 2 ERPPCs every 30 seconds, so something had to be done. To this end, the implementation of 1.4 Heat Sinks and Ghost Heat was well intended and somewhat effective, though they missed the core issue.
The current MWO heat model is a linear equation based purely on the number of heat sinks with a multiplier for map heat level. The best example of how this works is here. As best as I can tell the function operates the same today. The equation is simply
Quote
y = - x * (Effective Heat Sinks / 10) + (Max Heat)
where
Quote
Max Heat = Effective Heat Sinks + 30
Effective Heat Sinks (EHS) is the total value of heat sinks, not necessarily the actual number of heat sinks. 20 Single Heat Sinks is 22 EHS. 20 Double Heat Sinks in the current game would be 20*1.4=28 EHS.
This means that heat will bleed at 0.1 Heat per Second, per Heat Sink.
Using this formula, there is a very large disconnect between the time to sink all heat with 10 heat sinks and 22 Double (1.4) heat sinks, let alone 22 true DHS (2.0). Using the above formula, 40 heat with 10 SHS will take 40 seconds to sink all heat. With 22 DHS (1.4) and at the max heat of 60.8, it will take about 24 seconds to drain the heat. If these were 22 DHS (2.0), the max heat would be 74 and it would take about 17 seconds to cool. If this were the case, one could fire 4 ERPPCs every 13 seconds and be heat neutral. Obviously this is too many PPCs at once way too often when a Mech with 10 single heat sinks can fire 2 ERPPCs every 30 seconds, so something had to be done. To this end, the implementation of 1.4 Heat Sinks and Ghost Heat was well intended and somewhat effective, though they missed the core issue.
EXPONENTIAL DECAY
Spoiler
Using the formula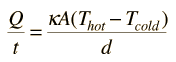 we can approximate real life heat dissipation. The constants in the formula would need to be tweaked to fit, of course, but this is a much better model to use for dissipating heat.
we can approximate real life heat dissipation. The constants in the formula would need to be tweaked to fit, of course, but this is a much better model to use for dissipating heat.
At higher heat levels the mech's temperature would drop quickly, allowing smaller and less heat intensive weapons to fire faster while still preventing high heat weapons from re-firing without risk of overheating. This is all the more prominent in single HS builds, as your heat would bleed much faster than it would using a linear equation. At moderate heat levels your weapon use would be about the same as it is now - fire any weapon but watch your heat and think before you alpha strike. At lower heat levels the temperature would drop much slower. This means that while you are relatively cool, you must be careful group firing a lot of weapons.
In order to examine this model , assume that the number of effective heat sinks is the maximum heat level for your mech. That means for 10 single heat sinks your max heat is 10. For 20 DHS your max heat is 40. The 30 base heat seen in MWO is not necessary here as heat levels will drop quickly and most builds will be unable to reach the higher heat thresholds with proper heat management. In addition, this forces pilots not to alpha with too many hot weapons.

To find the variables that work the best for Battletech weapons and heat sinks, I started with the thermal conductivity (K) value for steel, 50, set the diameter and surface area to 1 so that they would cancel out , and rewrote the equation to Q/t = k*A(Th-Tc)/d which equals Q/t = k*(Th-Tc).
From this I just multiply by the constant 0.000526565076466 to get from watt seconds to Celsius heat units (Note this is not the same as degrees Celsius). Whether this part is right or not does not matter, as the important aspect of this math is the heat transfer rate dH/dt and since the heat in battletech is some arbitrary unit, the conversion from Celsius heat units to Battletech Heat Units is just a constant multiplier.
To get the right heat transfer rate I created an approximation for the thermal conductivity based on the equation
kModified = (k + eHS * kC1 + kC2 / eHS) * HSmult * MassMult * globalCon
where
k = 50.2 (steel)
kC1 = 25 (best fit by trial and error)
kC2 = 1000 (best fit by trial and error)
eHS = effective heat sinks
and multipliers for number of heat sinks, mass of mech, and the global conductivity of the map.
I added the multipliers to limit the gap between high and low eHS builds and high and low mech tonnages. The body of a 100 ton mech will generally be thicker than the body of a 20 ton mech so the heat will transfer heat away at a lower rate. At the same time, heat sinks in a mech will operate less efficiently the more there are. Keep in mind that these two multipliers are approximations and have been tweaked to work best with the rest of the formula. It would be exceedingly difficult to calculate actual efficiency and heat dissipation for every single mech so I have approximated it here.
HSmult = f(eHS) with HSmult = 1 at 10 eHS and HSmult = 0.7 for 44 eHS
MassMult = f(mass) with MassMult = 1.2 at 20 tons and MassMult = 0.9 at 100 tons.
At this time, the global conductivity (also a gross approximation of thermal convection) which is dependent on numerous atmospheric conditions that would be difficult to simulate is set to 0.75 by default and in these examples.
Using the formula
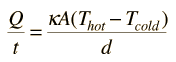 we can approximate real life heat dissipation. The constants in the formula would need to be tweaked to fit, of course, but this is a much better model to use for dissipating heat.
we can approximate real life heat dissipation. The constants in the formula would need to be tweaked to fit, of course, but this is a much better model to use for dissipating heat.At higher heat levels the mech's temperature would drop quickly, allowing smaller and less heat intensive weapons to fire faster while still preventing high heat weapons from re-firing without risk of overheating. This is all the more prominent in single HS builds, as your heat would bleed much faster than it would using a linear equation. At moderate heat levels your weapon use would be about the same as it is now - fire any weapon but watch your heat and think before you alpha strike. At lower heat levels the temperature would drop much slower. This means that while you are relatively cool, you must be careful group firing a lot of weapons.
In order to examine this model , assume that the number of effective heat sinks is the maximum heat level for your mech. That means for 10 single heat sinks your max heat is 10. For 20 DHS your max heat is 40. The 30 base heat seen in MWO is not necessary here as heat levels will drop quickly and most builds will be unable to reach the higher heat thresholds with proper heat management. In addition, this forces pilots not to alpha with too many hot weapons.

To find the variables that work the best for Battletech weapons and heat sinks, I started with the thermal conductivity (K) value for steel, 50, set the diameter and surface area to 1 so that they would cancel out , and rewrote the equation to Q/t = k*A(Th-Tc)/d which equals Q/t = k*(Th-Tc).
From this I just multiply by the constant 0.000526565076466 to get from watt seconds to Celsius heat units (Note this is not the same as degrees Celsius). Whether this part is right or not does not matter, as the important aspect of this math is the heat transfer rate dH/dt and since the heat in battletech is some arbitrary unit, the conversion from Celsius heat units to Battletech Heat Units is just a constant multiplier.
To get the right heat transfer rate I created an approximation for the thermal conductivity based on the equation
kModified = (k + eHS * kC1 + kC2 / eHS) * HSmult * MassMult * globalCon
where
k = 50.2 (steel)
kC1 = 25 (best fit by trial and error)
kC2 = 1000 (best fit by trial and error)
eHS = effective heat sinks
and multipliers for number of heat sinks, mass of mech, and the global conductivity of the map.
I added the multipliers to limit the gap between high and low eHS builds and high and low mech tonnages. The body of a 100 ton mech will generally be thicker than the body of a 20 ton mech so the heat will transfer heat away at a lower rate. At the same time, heat sinks in a mech will operate less efficiently the more there are. Keep in mind that these two multipliers are approximations and have been tweaked to work best with the rest of the formula. It would be exceedingly difficult to calculate actual efficiency and heat dissipation for every single mech so I have approximated it here.
HSmult = f(eHS) with HSmult = 1 at 10 eHS and HSmult = 0.7 for 44 eHS
MassMult = f(mass) with MassMult = 1.2 at 20 tons and MassMult = 0.9 at 100 tons.
At this time, the global conductivity (also a gross approximation of thermal convection) which is dependent on numerous atmospheric conditions that would be difficult to simulate is set to 0.75 by default and in these examples.
CONDITIONS
For the most part, we know what firing certain weapons does to us and how hot we get with the linear model. What we do not know is how these weapons would behave under an exponential decay model. To better visualize this, I have written a VBA macro in excel to simulate heat under a number of conditions. Keep in mind that this tool is more accurate the smaller the time increments are set and that laser duration is only as accurate as the time increment.
Weapon Heat
Spoiler
Condition 1:
Locust 3M: 4x SLas (2 heat), 1x MLas (4 heat), 20 tons, 10 SHS
Initial heat = 0. Alpha strike at t=1.

Runs hot with an alpha strike but cools down to half capacity pretty quickly
Condition 2:
Locust 3M: 4x SLas (2 heat), 1x MLas (4 heat), 20 tons, 10 SHS
Initial heat = 10. 8 heat every 8 seconds (4 times)

Condition 3:
Locust 3M: 4x SLas (2 heat), 1x MLas (4 heat), 20 tons, 10 SHS
Initial heat = 0. 4 heat every 2 seconds (8 times)

This is where the differences between the two systems really stands out. Continual fire with the linear system will always overheat or stabilize by waiting for a full cooldown. Continual fire with the exponential system will reach a peak where the change in heat over time approaches zero.
Remember that the with the linear model the max heat is 30 plus the effective heat sinks. If this was the same for the exponential model the heat would dissipate too quickly at high levels to make a difference.
Yes this stock locust still runs hot but it will no longer melt with single heat sinks. It goes without saying that double heat sinks would be a huge improvement, but they are no longer a prerequisite for survival (though it is still a locust, so survival is probably not something that pilot is thinking of)
Condition 4:
Jenner F(C): 3x MLas (4 heat), 3x SLas (2 heat), 35 tons, 15 DHS
Initial heat = 0. Alpha strike at t=1.

That is plenty cool.
Condition 5:
Jenner F(C): 3x MLas (4 heat), 3x SLas (2 heat), 35 tons, 15 DHS
Initial heat = 0. 18 heat every 4 seconds (8 times)

You do not have to worry about very much with this mech. The effective HPS generated by the weapons is ~5, so the heat levels tend to max out just under 14 heat.
Okay, let's look at a really hot stock mech, the Nova Prime. With only 18 double heat sinks (36 eHS) this mech will obviously overheat with an alpha strike of 60 heat, so how about some link fire examples.
Condition 6:
Nova Prime: 12x cERMLas (5 heat), 50 tons, 18 DHS
Initial heat = 0. 30 heat every 4 seconds (5 times)

This is the equivalent of firing one arm of 6 cERML just about continually (slight pause there). The heat level maxes out at about 36, just under the max heat for the nova. This is redlining it but you will not suicide in a normal fight.
Condition 7:
Nova Prime: 12x cERMLas (5 heat), 50 tons, 18 DHS
Initial heat = 0. 15 heat every 2 seconds (8 times)

This is almost a constant rate of fire (3 lasers at a time) without overheating.
With this system the stock nova is a viable option of melting other's faces without melting your own into slag.
Now how about a relatively cool mech, the Centurion A(C)
Condition 8:
CN9-A(C): 2x MPL (4.6 heat), 3x SRM4 + Artemis (3 heat) 50 tons, 11 DHS
Initial heat = 0. 18.2 heat every 3.5 seconds (8 times)

This is an approximation of firing as quickly as possible. SRMs reload in 3 seconds and medium pulse lasers can only fire once every 3.6 seconds, but the point remains. This mech will still overheat if the pilot is not careful
Condition 9:
Hunchback 4P: 8x MLas (4 heat), 1x SLas 2 heat) 50 tons, 23 SHS
Initial heat = 0. 32 heat every 6 seconds (8 times)

Ow. Well that result is still the same, even with waiting an extra 2 second between salvos. What if we only fire the torso mounted lasers?
Condition 10:
Hunchback 4P: 8x MLas (4 heat), 1x SLas 2 heat) 50 tons, 23 SHS
Initial heat = 0. 24 heat every 6 seconds (8 times)

Better. We are still a little too hot (maxes out a little over 24 heat, 23 heat would be the max) so we would only be able to fire JUST the 6 side torso lasers every 7+ seconds.
What if we do the same tests using the Champion version of this mech which uses DHS?
Condition 11:
Hunchback 4P: 9x MLas (4 heat), 50 tons, 18 DHS
Initial heat = 0. 32 heat every 6 seconds (8 times) (NOTE we are only firing 8 lasers still, same as previous test.

Significantly less face-melty. Since the 18 DHS give us a max heat of 36 I bet we can fire all 9 every 6 seconds.
Condition 12:
Hunchback 4P: 9x MLas (4 heat), 50 tons, 18 DHS
Initial heat = 0. 36 heat every 6 seconds (8 times)

Okay, let's try some PPCs!
Condition 13:
Awesome 8Q: 3x PPC (10 heat), 1x SLas (2 heat), 80 tons, 28 SHS
Initial heat = 0. 30 heat every 4 seconds (8 times)

The pilot needs to exercise caution when firing. He will overheat at the second alpha strike. In other news the Awesome may be worth something again. What if those were ERPPCs and DHS?
Condition 14:
Awesome 8Q (modified): 3x ERPPC (15 heat), 1x SLas (2 heat), 80 tons, 19 DHS
Initial heat = 0. 45 heat every 4 seconds (8 times)

No need for ghost heat here!!
Remember the doom of the PPC Stalker?
Condition 15:
Stalker 3F (PPC): 4x PPC (10 heat), 85 tons, 20 DHS
Initial heat = 0. 40 heat every 4 seconds (8 times)

The mech WILL get a shutdown warning at the first alpha strike in hotter areas and will probably damage itself with the second alpha. Since this mech produces 40 heat per alpha and has 40 eHS, how long does the pilot have to wait to fire again?
Condition 16:
Stalker 3F (PPC): 4x PPC (10 heat), 85 tons, 20 DHS
Initial heat = 0. 40 heat every 8 seconds (8 times)

About 8 seconds. That is a long time in a battle. The pilot is much better off link firing 2 at a time.
How about a stock PPC monster like the Warhawk Prime? 60 heat from the 4 cERPPCs is way too much to even bother with, so let's try link firing in pairs.
Condition 17:
Warhawk Prime: 4x cERPPC (15 heat), 1x cLRM15 (4 heat) 85 tons, 20 DHS
Initial heat = 0. 30 heat every 2 seconds (8 times)

Still too much. Chain firing every other second?
Condition 18:
Warhawk Prime: 4x cERPPC (15 heat), 1x cLRM10 (4 heat) 85 tons, 20 DHS
Initial heat = 0. 15 heat every 2 seconds (8 times)

That is do-able. What if we replaced the targeting computer and lrm 10 with extra heat sinks?
Condition 19:
Warhawk Prime: 4x cERPPC (15 heat), 85 tons, 28 DHS
Initial heat = 0. 30 heat every 2 seconds (8 times)

That is barely keeping it cool. At 56 eHS I should point out that the HS efficiency is down to 0.59
Now before we look at the Dire Wolf, I should point out that for a number of weapons the heat is not scaled like the damage or damage per second. The TT value for cUAC/5's is 1 heat and it is the same in game, making it one of the coolest weapons in game for the DPS it does. cERLL are actually cooler than the TT value, making it also stand out when looking at TT heat sink numbers.
Condition 20:
Dire Wolf Prime: 4x cERLL (9 heat), 4x cMPL (5.5 heat), 2x cUAC/5 (1 heat), 1x cLRM 10 ( 4 heat) 100 tons, 22 DHS
Initial heat = 0. 36 heat every 5.5 seconds (8 times) (firing 4x large lasers)

44 eHS is adequate for this mech until you start firing other weapons.
Condition 21:
Dire Wolf Prime: 4x cERLL (9 heat), 4x cMPL (5.5 heat), 2x cUAC/5 (1 heat), 1x cLRM 10 ( 4 heat) 100 tons, 22 DHS
Initial heat = 0. 58 heat every 5.5 seconds (8 times) (firing ALL lasers)

This will burn you
Okay, last one. What if you put 4 cERLL on a Dire Wolf and maxed out the heat sinks with nothing else on the mech? This wastes a lot of space in both free tonnage and by having more heat sinks than you will ever use, but it demonstrates what happens to your heat levels if you have lots of heat sinks with only moderate heat generation.
Condition 22:
Dire Wolf: 4x cERLL (9 heat), 100 tons, 33 DHS (efficiency 0.51) (t interval = 0.25s)
Initial heat = 0. 18 heat every 2.25 seconds (8 times)

And if only 1 laser is fired every 5.5 seconds.....

Now THIS is where you really see a difference. PGI said that they were increasing the heat of the Clan ER Large Laser because on some high heat sink builds it barely registered. This is not a fault of the heat of the weapon, but a fault of the heat system itself - having heat dissipation independent of heat levels actually prevents heat buildup. With exponential decay you will generate heat no matter how many heat sinks you have.
Unfortunately due to the complexity of firing multiple different weapons as soon as they become available cannot be simulated by this calculator. That would require me putting significantly more time into this and frankly, I am not getting paid for my work. You should see by now the trend of what this system can do
Condition 1:
Locust 3M: 4x SLas (2 heat), 1x MLas (4 heat), 20 tons, 10 SHS
Initial heat = 0. Alpha strike at t=1.

Runs hot with an alpha strike but cools down to half capacity pretty quickly
Condition 2:
Locust 3M: 4x SLas (2 heat), 1x MLas (4 heat), 20 tons, 10 SHS
Initial heat = 10. 8 heat every 8 seconds (4 times)

Condition 3:
Locust 3M: 4x SLas (2 heat), 1x MLas (4 heat), 20 tons, 10 SHS
Initial heat = 0. 4 heat every 2 seconds (8 times)

This is where the differences between the two systems really stands out. Continual fire with the linear system will always overheat or stabilize by waiting for a full cooldown. Continual fire with the exponential system will reach a peak where the change in heat over time approaches zero.
Remember that the with the linear model the max heat is 30 plus the effective heat sinks. If this was the same for the exponential model the heat would dissipate too quickly at high levels to make a difference.
Yes this stock locust still runs hot but it will no longer melt with single heat sinks. It goes without saying that double heat sinks would be a huge improvement, but they are no longer a prerequisite for survival (though it is still a locust, so survival is probably not something that pilot is thinking of)
Condition 4:
Jenner F(C): 3x MLas (4 heat), 3x SLas (2 heat), 35 tons, 15 DHS
Initial heat = 0. Alpha strike at t=1.

That is plenty cool.
Condition 5:
Jenner F(C): 3x MLas (4 heat), 3x SLas (2 heat), 35 tons, 15 DHS
Initial heat = 0. 18 heat every 4 seconds (8 times)

You do not have to worry about very much with this mech. The effective HPS generated by the weapons is ~5, so the heat levels tend to max out just under 14 heat.
Okay, let's look at a really hot stock mech, the Nova Prime. With only 18 double heat sinks (36 eHS) this mech will obviously overheat with an alpha strike of 60 heat, so how about some link fire examples.
Condition 6:
Nova Prime: 12x cERMLas (5 heat), 50 tons, 18 DHS
Initial heat = 0. 30 heat every 4 seconds (5 times)

This is the equivalent of firing one arm of 6 cERML just about continually (slight pause there). The heat level maxes out at about 36, just under the max heat for the nova. This is redlining it but you will not suicide in a normal fight.
Condition 7:
Nova Prime: 12x cERMLas (5 heat), 50 tons, 18 DHS
Initial heat = 0. 15 heat every 2 seconds (8 times)

This is almost a constant rate of fire (3 lasers at a time) without overheating.
With this system the stock nova is a viable option of melting other's faces without melting your own into slag.
Now how about a relatively cool mech, the Centurion A(C)
Condition 8:
CN9-A(C): 2x MPL (4.6 heat), 3x SRM4 + Artemis (3 heat) 50 tons, 11 DHS
Initial heat = 0. 18.2 heat every 3.5 seconds (8 times)

This is an approximation of firing as quickly as possible. SRMs reload in 3 seconds and medium pulse lasers can only fire once every 3.6 seconds, but the point remains. This mech will still overheat if the pilot is not careful
Condition 9:
Hunchback 4P: 8x MLas (4 heat), 1x SLas 2 heat) 50 tons, 23 SHS
Initial heat = 0. 32 heat every 6 seconds (8 times)

Ow. Well that result is still the same, even with waiting an extra 2 second between salvos. What if we only fire the torso mounted lasers?
Condition 10:
Hunchback 4P: 8x MLas (4 heat), 1x SLas 2 heat) 50 tons, 23 SHS
Initial heat = 0. 24 heat every 6 seconds (8 times)

Better. We are still a little too hot (maxes out a little over 24 heat, 23 heat would be the max) so we would only be able to fire JUST the 6 side torso lasers every 7+ seconds.
What if we do the same tests using the Champion version of this mech which uses DHS?
Condition 11:
Hunchback 4P: 9x MLas (4 heat), 50 tons, 18 DHS
Initial heat = 0. 32 heat every 6 seconds (8 times) (NOTE we are only firing 8 lasers still, same as previous test.

Significantly less face-melty. Since the 18 DHS give us a max heat of 36 I bet we can fire all 9 every 6 seconds.
Condition 12:
Hunchback 4P: 9x MLas (4 heat), 50 tons, 18 DHS
Initial heat = 0. 36 heat every 6 seconds (8 times)

Okay, let's try some PPCs!
Condition 13:
Awesome 8Q: 3x PPC (10 heat), 1x SLas (2 heat), 80 tons, 28 SHS
Initial heat = 0. 30 heat every 4 seconds (8 times)

The pilot needs to exercise caution when firing. He will overheat at the second alpha strike. In other news the Awesome may be worth something again. What if those were ERPPCs and DHS?
Condition 14:
Awesome 8Q (modified): 3x ERPPC (15 heat), 1x SLas (2 heat), 80 tons, 19 DHS
Initial heat = 0. 45 heat every 4 seconds (8 times)

No need for ghost heat here!!
Remember the doom of the PPC Stalker?
Condition 15:
Stalker 3F (PPC): 4x PPC (10 heat), 85 tons, 20 DHS
Initial heat = 0. 40 heat every 4 seconds (8 times)

The mech WILL get a shutdown warning at the first alpha strike in hotter areas and will probably damage itself with the second alpha. Since this mech produces 40 heat per alpha and has 40 eHS, how long does the pilot have to wait to fire again?
Condition 16:
Stalker 3F (PPC): 4x PPC (10 heat), 85 tons, 20 DHS
Initial heat = 0. 40 heat every 8 seconds (8 times)

About 8 seconds. That is a long time in a battle. The pilot is much better off link firing 2 at a time.
How about a stock PPC monster like the Warhawk Prime? 60 heat from the 4 cERPPCs is way too much to even bother with, so let's try link firing in pairs.
Condition 17:
Warhawk Prime: 4x cERPPC (15 heat), 1x cLRM15 (4 heat) 85 tons, 20 DHS
Initial heat = 0. 30 heat every 2 seconds (8 times)

Still too much. Chain firing every other second?
Condition 18:
Warhawk Prime: 4x cERPPC (15 heat), 1x cLRM10 (4 heat) 85 tons, 20 DHS
Initial heat = 0. 15 heat every 2 seconds (8 times)

That is do-able. What if we replaced the targeting computer and lrm 10 with extra heat sinks?
Condition 19:
Warhawk Prime: 4x cERPPC (15 heat), 85 tons, 28 DHS
Initial heat = 0. 30 heat every 2 seconds (8 times)

That is barely keeping it cool. At 56 eHS I should point out that the HS efficiency is down to 0.59
Now before we look at the Dire Wolf, I should point out that for a number of weapons the heat is not scaled like the damage or damage per second. The TT value for cUAC/5's is 1 heat and it is the same in game, making it one of the coolest weapons in game for the DPS it does. cERLL are actually cooler than the TT value, making it also stand out when looking at TT heat sink numbers.
Condition 20:
Dire Wolf Prime: 4x cERLL (9 heat), 4x cMPL (5.5 heat), 2x cUAC/5 (1 heat), 1x cLRM 10 ( 4 heat) 100 tons, 22 DHS
Initial heat = 0. 36 heat every 5.5 seconds (8 times) (firing 4x large lasers)

44 eHS is adequate for this mech until you start firing other weapons.
Condition 21:
Dire Wolf Prime: 4x cERLL (9 heat), 4x cMPL (5.5 heat), 2x cUAC/5 (1 heat), 1x cLRM 10 ( 4 heat) 100 tons, 22 DHS
Initial heat = 0. 58 heat every 5.5 seconds (8 times) (firing ALL lasers)

This will burn you
Okay, last one. What if you put 4 cERLL on a Dire Wolf and maxed out the heat sinks with nothing else on the mech? This wastes a lot of space in both free tonnage and by having more heat sinks than you will ever use, but it demonstrates what happens to your heat levels if you have lots of heat sinks with only moderate heat generation.
Condition 22:
Dire Wolf: 4x cERLL (9 heat), 100 tons, 33 DHS (efficiency 0.51) (t interval = 0.25s)
Initial heat = 0. 18 heat every 2.25 seconds (8 times)

And if only 1 laser is fired every 5.5 seconds.....

Now THIS is where you really see a difference. PGI said that they were increasing the heat of the Clan ER Large Laser because on some high heat sink builds it barely registered. This is not a fault of the heat of the weapon, but a fault of the heat system itself - having heat dissipation independent of heat levels actually prevents heat buildup. With exponential decay you will generate heat no matter how many heat sinks you have.
Unfortunately due to the complexity of firing multiple different weapons as soon as they become available cannot be simulated by this calculator. That would require me putting significantly more time into this and frankly, I am not getting paid for my work. You should see by now the trend of what this system can do
Jump Jets
Spoiler
This is a heat-generating piece of equipment and will affect the mech as much as any small weapon. For MWO values this is very small and will hardly affect any mech unless firing puts the mech over the edge of overheating. Class V jump jets generate 0.1 heat per second per JJ. On a Spider 5V with 10 SHS this results in...

A zero heat buildup for the linear model and a little over 2 heat for 3 seconds of burn time. This is actually not too bad. TT values (iirc) say 2 heat per jump jet which is really hot for the little spider (below).

This is a heat-generating piece of equipment and will affect the mech as much as any small weapon. For MWO values this is very small and will hardly affect any mech unless firing puts the mech over the edge of overheating. Class V jump jets generate 0.1 heat per second per JJ. On a Spider 5V with 10 SHS this results in...

A zero heat buildup for the linear model and a little over 2 heat for 3 seconds of burn time. This is actually not too bad. TT values (iirc) say 2 heat per jump jet which is really hot for the little spider (below).

Flamers
Spoiler
This is a big one. I will not even attempt to bother with how MWO flamers currently work and reverse engineer them to work with this model. I assume they increase your ambient heat by a certain percentage and stacking a small damage modifier. Instead I started fresh. It took a lot of tweaking but I think I found something that works relatively well against all targets and then extremely well against targets with low eHS counts.
My version: Directly increase the ambient temperature by 1 per flamer, add 0.25 heat per second per flamer, does 0 actual damage. At the same time the flamer does 2 HPS to the person firing it, making prolonged salvos unwise. With the increased combat effectiveness of flamers I decided that this would be enough. For my examples I will use the Hunchback 4P(C) and Nova PRIME, both 50 ton mechs, with flamers replacing all medium lasers.
Condition 26:
Hunchback 4P(C): 9x Flamer (2 heat), 50 tons, 18 DHS
Initial heat = 0. 18 heat every 1 seconds (8 times)

With all 15 DHS our Hunchback will overheat after firing all for 3 seconds. Let's see what this did to a Locust 3M. Remember, a 20 ton mech with only 10 eHS will have the best heat sink efficiency.
Condition 27:
Locust 3M: 20 tons, 10 SHS (target)
Initial heat = 0. Ambient heat = 9. Heat damage = 2.25/s

This makes the bug all toasty but it will not overheat unless it is in an inherently hot environment or it decides to fire while this hot. Remember that the Locust is a fast mech and IF it can be hit with all 9 flamers for 3 seconds, the hunchback is heating itself up and is vulnerable to enemy fire. Most mechs (custom or other) have more than 10 SHS so let's try a different target.
Condition 28:
Jenner F(C): 35 tons, 15 DHS (target)
Initial heat = 0. Ambient heat = 9. Heat damage = 2.25/s

Again the Jenner does not overheat but it sure gives the pilot something to think about. What if the Jenner has already fired?
Condition 29:
Jenner F(C): 35 tons, 15 DHS (target)
Initial heat = 18. Ambient heat = 9. Heat damage = 2.25/s

Well that looks different. The flamers actually slow down heat dissipation because the initial heat is above the level of zero dH/dt. Time your shots right and a couple flamers could make all the difference.
Condition 30:
Nova: 12x Flamer (2 heat), 50 tons, 18 DHS
Initial heat = 0. 24 heat every 1 seconds (8 times)

The Nova will overheat after firing for about 2.5 seconds.
Condition 31:
Locust 3M: 20 tons, 10 SHS (target)
Initial heat = 0. Ambient heat = 12. Heat damage = 3/s

The Locust overheats just after 1 second and finally restarts after about 4.5 of being offline. That will leave a mark. Then again, so will 6-12 cERML.
Condition 32:
Jenner F(C): 35 tons, 15 DHS (target)
Initial heat = 0. Ambient heat = 12. Heat damage = 3/s

Hot, but not always deadly.
Condition 33:
Jenner F(C): 35 tons, 15 DHS (target)
Initial heat = 18. Ambient heat = 12. Heat damage = 3/s

This is a big one. I will not even attempt to bother with how MWO flamers currently work and reverse engineer them to work with this model. I assume they increase your ambient heat by a certain percentage and stacking a small damage modifier. Instead I started fresh. It took a lot of tweaking but I think I found something that works relatively well against all targets and then extremely well against targets with low eHS counts.
My version: Directly increase the ambient temperature by 1 per flamer, add 0.25 heat per second per flamer, does 0 actual damage. At the same time the flamer does 2 HPS to the person firing it, making prolonged salvos unwise. With the increased combat effectiveness of flamers I decided that this would be enough. For my examples I will use the Hunchback 4P(C) and Nova PRIME, both 50 ton mechs, with flamers replacing all medium lasers.
Condition 26:
Hunchback 4P(C): 9x Flamer (2 heat), 50 tons, 18 DHS
Initial heat = 0. 18 heat every 1 seconds (8 times)

With all 15 DHS our Hunchback will overheat after firing all for 3 seconds. Let's see what this did to a Locust 3M. Remember, a 20 ton mech with only 10 eHS will have the best heat sink efficiency.
Condition 27:
Locust 3M: 20 tons, 10 SHS (target)
Initial heat = 0. Ambient heat = 9. Heat damage = 2.25/s

This makes the bug all toasty but it will not overheat unless it is in an inherently hot environment or it decides to fire while this hot. Remember that the Locust is a fast mech and IF it can be hit with all 9 flamers for 3 seconds, the hunchback is heating itself up and is vulnerable to enemy fire. Most mechs (custom or other) have more than 10 SHS so let's try a different target.
Condition 28:
Jenner F(C): 35 tons, 15 DHS (target)
Initial heat = 0. Ambient heat = 9. Heat damage = 2.25/s

Again the Jenner does not overheat but it sure gives the pilot something to think about. What if the Jenner has already fired?
Condition 29:
Jenner F(C): 35 tons, 15 DHS (target)
Initial heat = 18. Ambient heat = 9. Heat damage = 2.25/s

Well that looks different. The flamers actually slow down heat dissipation because the initial heat is above the level of zero dH/dt. Time your shots right and a couple flamers could make all the difference.
Condition 30:
Nova: 12x Flamer (2 heat), 50 tons, 18 DHS
Initial heat = 0. 24 heat every 1 seconds (8 times)

The Nova will overheat after firing for about 2.5 seconds.
Condition 31:
Locust 3M: 20 tons, 10 SHS (target)
Initial heat = 0. Ambient heat = 12. Heat damage = 3/s

The Locust overheats just after 1 second and finally restarts after about 4.5 of being offline. That will leave a mark. Then again, so will 6-12 cERML.
Condition 32:
Jenner F(C): 35 tons, 15 DHS (target)
Initial heat = 0. Ambient heat = 12. Heat damage = 3/s

Hot, but not always deadly.
Condition 33:
Jenner F(C): 35 tons, 15 DHS (target)
Initial heat = 18. Ambient heat = 12. Heat damage = 3/s

Weapon values
Spoiler
In order to better facilitate this model and balance the game in general, a lot of the weapon values need to be modified. While this is largely a separate issue, the heat and HPS aspects are very relevant and in some cases necessary for any kind of heat balance.
In addition, I have added cone-of-fire values which would help with the PPFLD without making it impossible to hit a target. (I already had those written down so why not)
These tables are separated by IS and Clan, then further separated by TT values (modified for balance), MWO values as of 8/26/14 (not modified), and then modified MWO values for balance. Deviations from standard values are in red.
I don't think I missed anything here...
Inner Sphere
Clan
In order to better facilitate this model and balance the game in general, a lot of the weapon values need to be modified. While this is largely a separate issue, the heat and HPS aspects are very relevant and in some cases necessary for any kind of heat balance.
In addition, I have added cone-of-fire values which would help with the PPFLD without making it impossible to hit a target. (I already had those written down so why not)
These tables are separated by IS and Clan, then further separated by TT values (modified for balance), MWO values as of 8/26/14 (not modified), and then modified MWO values for balance. Deviations from standard values are in red.
I don't think I missed anything here...
Inner Sphere
Spoiler


Clan
Other options
Spoiler
While I believe that this is the best model to use for heat balance, it may not be the best solution. There are other variables that can be changed or tested in conjunction with the exponential heat decay formula.
1. Flat heat level - Make the max heat for all mechs a constant value, say 30.
2. Flat heat modifier - Add a positive or negative value to modify the max heat level given by effective heat sinks.
3. Larger efficiency gap - increase the negative slope in the heat effeciency equation. The same can be done with the weight multiplier
4. Add a modifier for heat based on number of weapons fired simultaneously. Not a lot, but enough to push most heat neutral mechs over the edge if they alpha strike. This part is not based on physics but is a "ghost heat" that is consistent and at least makes sense.
New heat=Heat+(16*(weapons-1))/SQRT((weapons-1)^2+20)
This part is included in the calculator in cells A40:B42 but is not connected to anything else.
5. Increase heat efficiency for shut down mechs. I did not add it in here but it could easily be doubled for shut down mechs (exterior temperatures like flamers and lava would still affect the mech)
6. I am sure there are more I have not thought of but the core concept of exponential decay remains the same.
While I believe that this is the best model to use for heat balance, it may not be the best solution. There are other variables that can be changed or tested in conjunction with the exponential heat decay formula.
1. Flat heat level - Make the max heat for all mechs a constant value, say 30.
2. Flat heat modifier - Add a positive or negative value to modify the max heat level given by effective heat sinks.
3. Larger efficiency gap - increase the negative slope in the heat effeciency equation. The same can be done with the weight multiplier
4. Add a modifier for heat based on number of weapons fired simultaneously. Not a lot, but enough to push most heat neutral mechs over the edge if they alpha strike. This part is not based on physics but is a "ghost heat" that is consistent and at least makes sense.
New heat=Heat+(16*(weapons-1))/SQRT((weapons-1)^2+20)
This part is included in the calculator in cells A40:B42 but is not connected to anything else.
5. Increase heat efficiency for shut down mechs. I did not add it in here but it could easily be doubled for shut down mechs (exterior temperatures like flamers and lava would still affect the mech)
6. I am sure there are more I have not thought of but the core concept of exponential decay remains the same.
Q & A
Spoiler
Q: Didn't PGI say that their heat dissipation is based on a 10 second turn in table top?
A: Yes, but all weapons can currently fire at least twice per 10 second time, essentially invalidating the current formula.
Q: Aren't heat sinks in battletech actually heat pumps, so that they work the same in any environment?
A: Yes, you are absolutely right about mech heat sinks. However, I am considering the transfer of heat from the weapons to the heat pumps that run through the mech, which is still an issue of thermal conductivity. Assume that the heat sinks themselves are effectively thermal reservoirs at zero BT heat units. We are looking at how quickly the heat transfers to the heat pumps (quicker for more because more heat "sinks" means more volume can "hold" and dissipate heat) without having to deal with the coefficient of performance (exponentially less % the smaller the temperature difference) from the ideal Carnot cycle. We could add in the transfer of heat in such pumps but that is another level of complexity. It is simpler to look at the mech (minus the heat sinks) as a single control volume and approximate from there.
Yes I know I added a global and local conductivity factor - The global at 0.75 is to adjust the formula easily and 0.75 seemed to fit the best to me. The local at 1 does nothing but could improve heat performance in water where the conductivity is higher.
Q: The current heat system is fine. Don't change it
A: Okay not really a question but I will still answer it. In the current heat model there is a very large gap between low and high eHS builds. SHS are all but useless and on smaller chassis, non-existent. Yes I realize that there are some builds that do fine with single heat sinks but under most circumstances it is not even a question to spend the money to upgrade. This system allows for true double heat sinks, removes ghost heat, and paves the way for a more scaled weapon balance. In order to best use this model I suggest implementing some form of weapon inaccuracy (cone of fire) to alleviate all the PPFLD we see possible under this model, but this is not necessarily a prerequisite and PPFLD remains another problem even now.
Q: I like the concept but disagree on the values
A: That is fine. I invite you to play around with the calculator yourself or use the equations and concepts to build your own. The core point is that the current heat system can be improved with exponential heat decay, not that these inputs are set in stone.
Q: Won't this make hot builds more forgiving?
A: Yes, but it will also make cool builds LESS forgiving, as any amount of heat generated would spike your levels up significantly.
Q: Is this just a big post to complain about ghost heat?
A: No. While I dislike ghost heat for violating the First Law of Thermodynamics, this post presents an alternative to the core MWO heat system on which ghost heat was based.
Yes I know it is a game, but this is science fiction, not fantasy, and any in game mechanic should be an approximation of physics or at the very least have some sort of grounding in it. On top of that, ghost heat is extremely unbalanced with regards to all the different weapon types, makes no sense mathematically (linearly or exponentially), and is largely unnecessary. Oh and something about the Second Law too...
Q: The current MWO heat scale has a dissipation rating of BT Tabletop - 1 heat point per heat sink in 10seconds. And of course because of real time, it has the threshold value (that causes problems and is the reason for Ghost Heat) - wouldn't be the often suggested lower heat cap - higher dissipation + heat scale penalties have the same or better effect as an exponential decay?
A: In the higher register it would be very similar to exponential decay but it still differs on a couple key points.
1.) Double heat sinks are truly double (not 1.4) and the difference in effectiveness between 10 single heat sinks and 10 double heat sinks is much lower. Remember they said doubles would never be true doubles outside of the engine because that would make mechs cool down too fast.
2.) Firing low heat level weapons or firing a single high heat weapon with a lot of heat sinks barely makes a blip on MWO's heat scale simply because the linear equation is a function of heat sinks and time. The exponential equation also factors in current heat level making any heat generation weapon actually generate heat. Remember they made the CERLL hotter because it barely registered on most Dire Wolf builds with lot of heat sinks. (See also condition 23)
Additionally, Jump Jets would create heat instead of slowing the rate of decay, flamers could and would behave differently...
3.) Heat at low levels would take a fair (but reasonable) amount of time to dissipate. That means if you had an instant alpha strike heat value equal to your effective heat sinks, you would still not be able to fire safely until it dropped almost all the way down. With a higher linear sink rate you could fire a lot more often. (I say instant meaning PPC or AC20. Because lasers generate all their heat over the course of their exposure time the max alpha heat level would be a little less).
Q: Exponential means also it will hardly reach zero right?
A: It depends on the exponential function. In my model I rounded to zero once the heat level reached 0.49, which does not take quite as long as you might think - it is usually only a little longer than it would take to bleed the heat linearly. Therin lies the price of firing alphas that put you at 100% heat.
Q: Didn't PGI say that their heat dissipation is based on a 10 second turn in table top?
A: Yes, but all weapons can currently fire at least twice per 10 second time, essentially invalidating the current formula.
Q: Aren't heat sinks in battletech actually heat pumps, so that they work the same in any environment?
A: Yes, you are absolutely right about mech heat sinks. However, I am considering the transfer of heat from the weapons to the heat pumps that run through the mech, which is still an issue of thermal conductivity. Assume that the heat sinks themselves are effectively thermal reservoirs at zero BT heat units. We are looking at how quickly the heat transfers to the heat pumps (quicker for more because more heat "sinks" means more volume can "hold" and dissipate heat) without having to deal with the coefficient of performance (exponentially less % the smaller the temperature difference) from the ideal Carnot cycle. We could add in the transfer of heat in such pumps but that is another level of complexity. It is simpler to look at the mech (minus the heat sinks) as a single control volume and approximate from there.
Yes I know I added a global and local conductivity factor - The global at 0.75 is to adjust the formula easily and 0.75 seemed to fit the best to me. The local at 1 does nothing but could improve heat performance in water where the conductivity is higher.
Q: The current heat system is fine. Don't change it
A: Okay not really a question but I will still answer it. In the current heat model there is a very large gap between low and high eHS builds. SHS are all but useless and on smaller chassis, non-existent. Yes I realize that there are some builds that do fine with single heat sinks but under most circumstances it is not even a question to spend the money to upgrade. This system allows for true double heat sinks, removes ghost heat, and paves the way for a more scaled weapon balance. In order to best use this model I suggest implementing some form of weapon inaccuracy (cone of fire) to alleviate all the PPFLD we see possible under this model, but this is not necessarily a prerequisite and PPFLD remains another problem even now.
Q: I like the concept but disagree on the values
A: That is fine. I invite you to play around with the calculator yourself or use the equations and concepts to build your own. The core point is that the current heat system can be improved with exponential heat decay, not that these inputs are set in stone.
Q: Won't this make hot builds more forgiving?
A: Yes, but it will also make cool builds LESS forgiving, as any amount of heat generated would spike your levels up significantly.
Q: Is this just a big post to complain about ghost heat?
A: No. While I dislike ghost heat for violating the First Law of Thermodynamics, this post presents an alternative to the core MWO heat system on which ghost heat was based.
Yes I know it is a game, but this is science fiction, not fantasy, and any in game mechanic should be an approximation of physics or at the very least have some sort of grounding in it. On top of that, ghost heat is extremely unbalanced with regards to all the different weapon types, makes no sense mathematically (linearly or exponentially), and is largely unnecessary. Oh and something about the Second Law too...
Q: The current MWO heat scale has a dissipation rating of BT Tabletop - 1 heat point per heat sink in 10seconds. And of course because of real time, it has the threshold value (that causes problems and is the reason for Ghost Heat) - wouldn't be the often suggested lower heat cap - higher dissipation + heat scale penalties have the same or better effect as an exponential decay?
A: In the higher register it would be very similar to exponential decay but it still differs on a couple key points.
1.) Double heat sinks are truly double (not 1.4) and the difference in effectiveness between 10 single heat sinks and 10 double heat sinks is much lower. Remember they said doubles would never be true doubles outside of the engine because that would make mechs cool down too fast.
2.) Firing low heat level weapons or firing a single high heat weapon with a lot of heat sinks barely makes a blip on MWO's heat scale simply because the linear equation is a function of heat sinks and time. The exponential equation also factors in current heat level making any heat generation weapon actually generate heat. Remember they made the CERLL hotter because it barely registered on most Dire Wolf builds with lot of heat sinks. (See also condition 23)
Additionally, Jump Jets would create heat instead of slowing the rate of decay, flamers could and would behave differently...
3.) Heat at low levels would take a fair (but reasonable) amount of time to dissipate. That means if you had an instant alpha strike heat value equal to your effective heat sinks, you would still not be able to fire safely until it dropped almost all the way down. With a higher linear sink rate you could fire a lot more often. (I say instant meaning PPC or AC20. Because lasers generate all their heat over the course of their exposure time the max alpha heat level would be a little less).
Q: Exponential means also it will hardly reach zero right?
A: It depends on the exponential function. In my model I rounded to zero once the heat level reached 0.49, which does not take quite as long as you might think - it is usually only a little longer than it would take to bleed the heat linearly. Therin lies the price of firing alphas that put you at 100% heat.
Excel macro and calculator
Spoiler
In case the download link gets remove (or does not work for you) you can set up your own version of this calculator in an *.xlsm file in Excel 2007+
Download Heat Calculator.xlsm
Instructions
Worksheet setup
VBA code
In case the download link gets remove (or does not work for you) you can set up your own version of this calculator in an *.xlsm file in Excel 2007+
Download Heat Calculator.xlsm
Instructions
Spoiler
This will walk you through the dialogue boxes in the calculator. The calculator also supports a conversion to SI units for reactor temp (add to whatever the actual reactor temp is) and cockpit temp (add to whatever the life support temp is). The option for SI units is not extensively tested or even used in my examples so I did not include it in the instructions. Simply click 'yes' and enter the BT heat to SI multipliers you want to use. The curves of the graphs will be the same no matter what.

This will walk you through the dialogue boxes in the calculator. The calculator also supports a conversion to SI units for reactor temp (add to whatever the actual reactor temp is) and cockpit temp (add to whatever the life support temp is). The option for SI units is not extensively tested or even used in my examples so I did not include it in the instructions. Simply click 'yes' and enter the BT heat to SI multipliers you want to use. The curves of the graphs will be the same no matter what.

Worksheet setup
Spoiler
If you do not download the workbook and instead wish to set up your own spreadsheet to use the macro, set up these two columns like this:

If you do not download the workbook and instead wish to set up your own spreadsheet to use the macro, set up these two columns like this:

VBA code
Spoiler
Enter this into a module and link to a button.
==============
This looks like a lot but the actual heat calculation was really simple. The rest is just fluff so it works in excel. Yes I know the code can be improved in a lot of ways but it works for its purpose.
Enter this into a module and link to a button.
Public Declare Sub Sleep Lib "kernel32" (ByVal dwmilliseconds As Long)
Sub heat()
Dim Q As Variant, time As Variant, seconds As Single, k As Variant, A As Variant, Th As Variant, Tc As Variant, d As Variant, _
kC1 As Variant, kC2 As Variant, kMod As Variant, HS As Variant, eHS As Variant, dhs_mult As Variant, Qmax As Single
Dim dHdTt As Variant, dT As Variant, dHdT As Variant, T As Variant, E As Variant, hsClass As Variant
Dim message As Variant, size As Variant, SI As Integer
Dim ambC As Variant, ambExt As Variant, ambInt As Variant, Hh_m As Variant, Hh_p As Variant
Dim basemax As Variant, maxH As Variant
Dim HSmult As Single, MassMult As Single, globalCon As Single, hsmUb As Variant, hsmLb As Variant, mmUb As Variant, mmLb As Variant
Dim threshold As Variant, series As Variant, index As Integer
Dim ws As Worksheet
Dim dh_shi As Single, t_shi As Single, d_shi As Single, h_shi As Single, rg_shi As Single, rt_shi As Single, hd_shi As Single
Dim x As Integer, y As Integer, last As Integer, i1 As Integer, i2 As Integer
Dim Tpgi As Variant, timepgi As Variant
Dim envMod As Single, envMult As Single, lCon As Single, inpt As Variant
Set ws = ActiveSheet
Q = ws.Range("B4")
tInterval = ws.Range("B5")
k = ws.Range("B6")
A = ws.Range("B7")
Th = ws.Range("B8")
Tc = ws.Range("B9")
d = ws.Range("B10")
kC1 = ws.Range("B11")
kC2 = ws.Range("B12")
kMod = ws.Range("B13")
HS = ws.Range("B14")
hsClass = ws.Range("B15")
dhs_mult = ws.Range("B16")
Hh_m = ws.Range("B17")
Hh_p = ws.Range("B18")
threshold = ws.Range("B19")
size = ws.Range("B20")
basemax = ws.Range("B21")
globalCon = ws.Range("B22")
hsmLb = ws.Range("B23")
hsmUb = ws.Range("B24")
mmLb = ws.Range("B25")
mmUb = ws.Range("B26")
t_shi = ws.Range("B29")
d_shi = ws.Range("B30")
h_shi = ws.Range("B31")
rg_shi = ws.Range("B32")
rt_shi = ws.Range("B33")
hd_shi = ws.Range("B34")
envMod = ws.Range("B36")
envMult = ws.Range("B37")
lCon = ws.Range("B38")
series = InputBox("Set dataset to modify by entering 1, 2, or 3", , "1")
If series <> 1 And series <> 2 And series <> 3 Then
Exit Sub
End If
message = MsgBox("Use SI units (Yes) or BT units (No) for heat.", vbYesNo)
If message = vbYes Then
SI = 1
Hh_m = InputBox("Input ratio of m heat to bt heat", , Hh_m)
Hh_p = InputBox("Input ratio of p heat to m heat in the form _:1", , Hh_p) 'extra
End If
HS = InputBox("Set number of heat sinks", , HS)
If HS = 0 Or HS = "" Then
Exit Sub
End If
message = MsgBox("Are these DHS?", vbYesNo)
If message = vbYes Then '6 = yes, 7 = no
hsClass = "double"
dhs_mult = InputBox("Set DHS multiplier for SHS", , dhs_mult)
message = MsgBox("Use true DHS for internal? (else use DHS multiplier you just input)", vbYesNo)
If message = vbYes Then
eHS = (HS - 10) * dhs_mult + 20
Else
eHS = dhs_mult * HS
End If
ws.Range("B15") = "double"
Else
hsClass = "single"
eHS = HS
ws.Range("B15") = "single"
End If
maxH = basemax + eHS
message = MsgBox("Set initial heat? (no = use default)", vbYesNo)
If message = vbYes Then
maxH = InputBox("Enter initial heat (unitless)", , maxH)
End If
Th = maxH
HSmult = -0.0088 * eHS + 1.0882
MassMult = -0.00375 * size + 1.275
size = InputBox("Input mass in 5t interval from 20 to 100", , size)
size = Application.WorksheetFunction.Round(size / 5, 0) * 5
If size < 20 Or mass > 100 Then
MsgBox "Wrong mass size", vbCritical
Exit Sub
End If
message = MsgBox("Modify any other values?" & vbNewLine & "See left side of worksheet", vbYesNo)
If message = vbYes Then
'Th = InputBox("Set initial heat level (unitless)", , Th)
Tc = InputBox("Set final heat level (unitless)", , Tc)
threshold = InputBox("Set proximity threshold to stop simulation." & vbNewLine & "Will stop when within X units of final level", , threshold)
message = MsgBox("Do you wish to modify formula variables?", vbYesNo)
If message = vbYes Then
'Q = InputBox("Set Q (heat transfer rate)", , Q)
k = InputBox("Set k (material constant, steel ~~ 50)" & vbNewLine & "This affects the modified HS k", , k)
A = InputBox("Set A (surface area m^2)", , A)
tInterval = InputBox("Set time interval for plotting graph.", , tInterval)
d = InputBox("Set standard material diameter (1m approximated)", , d)
End If
'HSmult = -0.0088 * eHS + 1.0882
'MassMult = -0.00375 * size + 1.275
globalCon = InputBox("Set global conductivity", , globalCon)
message = MsgBox("Change local conditions?", vbYesNo)
If message = vbYes Then
inpt = InputBox("Set local conductivity", , lCon)
lCon = inpt
inpt = InputBox("Set temperature offset (unitless)", , envMod)
envMod = inpt
inpt = InputBox("Set quirk modifier (decimal percent)", , envMult)
envMult = inpt
End If
message = MsgBox("Change multipliers?", vbYesNo)
If message = vbYes Then
message = MsgBox("Use formula for HS inputs? (No = input value)", vbYesNo)
If message = vbYes Then
hsmLb = InputBox("Set value for max (44) eHS", , hsmLb)
hsmUb = InputBox("Set value for min (10) eHS", , hsmUb)
Else
HSmult = InputBox("Set HS multiplier." & vbNewLine & "Default = " & hsmUb & _
" for 10 eHS, " & hsmLb & " for 44 eHS", , HSmult)
End If
message = MsgBox("Use formula for mass inputs? (No = input value)", vbYesNo)
If message = vbYes Then
mmLb = InputBox("Set value for max t (100)t", , mmLb)
mmUb = InputBox("Set value for min t (20)t", , mmUb)
Else
MassMult = InputBox("Set size multiplier." & vbNewLine & "Default = " & mmUb & " for 20t," _
& mmLb & " for 100t", , MassMult)
End If
End If
message = MsgBox("Add secondary heat increase (SHI)?", vbYesNo)
If message = vbYes Then
t_shi = InputBox("Input time of SHI (in s)", , t_shi)
d_shi = InputBox("Input duration of SHI (in s)", , d_shi)
h_shi = InputBox("Input final size of SHI (in unitless form)", , h_shi)
rt_shi = InputBox("Input number of times to repeat SHI", , rt_shi)
rg_shi = InputBox("Input time gap between repeating SHI (in s)", , rg_shi)
hd_shi = InputBox("Input adjusted cooling temperature (in unitless form)", , hd_shi)
If d_shi > 0 Then
dh_shi = h_shi / d_shi
dh_shi = dh_shi / tInterval
Else
dh_shi = 0
End If
Else
t_shi = 0
d_shi = 0
h_shi = 0
dh_shi = 0
End If
End If
If d_shi < tInterval Then
d_shi = tInterval
End If
dh_shi = h_shi / d_shi
dh_shi = dh_shi * tInterval
HSmult = hsmLb - (hsmLb - hsmUb) / (44 - 10) * (eHS - 10) 'interpolate
MassMult = mmLb - (mmLb - mmUb) / (100 - 20) * (size - 20) 'interpolate
kMod = (k + eHS * kC1 + kC2 / eHS) * HSmult * MassMult * globalCon 'modified K value for HS
Tc = (Tc + envMod) * envMult * lCon
hd_shi = Tc + hd_shi
i1 = 0
i2 = 0
seconds = 0
index = 0
ReDim T(0 To index)
ReDim time(0 To index)
ReDim Tpgi(0 To index)
ReDim timepgi(0 To index)
T(0) = Th
time(0) = 0
Tpgi(0) = Th
While T(index) > threshold Or i2 <= rt_shi
seconds = Application.WorksheetFunction.Round(seconds + tInterval, 2)
index = index + 1
ReDim Preserve T(0 To index)
ReDim Preserve time(0 To index)
ReDim Preserve Tpgi(0 To index)
time(index) = seconds
Q = (kMod * A * (T(index - 1) - Tc) / d) * (tInterval)
If Qmax < Q Then
Qmax = Q
End If
If seconds >= t_shi And seconds < t_shi + d_shi Then
T(index) = T(index - 1) + dh_shi
Tpgi(index) = Tpgi(index - 1) + dh_shi
'dHdT = dHdT + dh_shi
Q = (kMod * A * (T(index) - hd_shi) / d) * (tInterval)
'Count = Count + 1
T(index) = T(index) - (Q * 0.000526565076466)
Tpgi(index) = Tpgi(index) - (eHS / 10) * tInterval
i1 = i1 + 1
Else
T(index) = T(index - 1) - (Q * 0.000526565076466) 'coefficient for energy to temperature
Tpgi(index) = Tpgi(index - 1) - (eHS / 10) * tInterval
End If
If T(index) < 0 Then
T(index) = 0
End If
If Tpgi(index) < 0 Then
Tpgi(index) = 0
End If
If i1 >= 1 And seconds >= t_shi + d_shi - tInterval And i2 < rt_shi Then 'trigger repeat
t_shi = t_shi + rg_shi
i1 = 1
i2 = i2 + 1
End If
If i1 >= 1 And seconds >= t_shi + d_shi And i2 <= rt_shi Then 'trigger wend
i2 = i2 + 1
End If
If seconds > 30 Then
GoTo printSeries
End If
'Application.Wait (Now + timealue("00:00:01"))
Wend
printSeries:
If series = 3 Then
x = 25
y = 6
ElseIf series = 2 Then
x = 15
y = 6
Else
x = 5
y = 6
End If
ws.Cells(y - 2, x + 1) = HSmult
ws.Cells(y - 2, x + 2) = MassMult
ws.Cells(y - 2, x + 3) = globalCon
ws.Cells(y - 4, x + 1) = size
ws.Cells(y - 4, x + 2) = eHS
ws.Cells(y - 4, x + 3) = kMod
ws.Cells(y - 4, x + 4) = Qmax
last = ws.Cells(Rows.Count, x).End(xlUp).Row
ws.Range(Cells(y, x), Cells(last, x + 8)).ClearContents
For index = 0 To UBound(time)
ws.Cells(y, x) = time(index)
If SI = 1 Then
ws.Cells(y, x + 1) = T(index) * Hh_p
Else
Hh_m = 1
End If
ws.Cells(y, x + 2) = T(index) * Hh_m
On Error Resume Next
ws.Cells(y, x + 3) = (T(index) * Hh_m - ws.Cells(y - 1, x + 2)) 'manually find dHdT to prevent subscript error
ws.Cells(y, x + 4) = (T(index)) / (basemax + eHS) * 100 'percentage
ws.Cells(y, x + 6) = Tpgi(index) * Hh_m
ws.Cells(y, x + 7) = Tpgi(index) - ws.Cells(y - 1, x + 6) * Hh_m 'dH/dT
ws.Cells(y, x + 8) = Tpgi(index) / (30 + eHS) * 100 'percentage
y = y + 1
'Sleep (tInterval * 800) 'milliseconds 'to simulate real time graphing - takes a long time for hot setups
Next
End Sub==============
This looks like a lot but the actual heat calculation was really simple. The rest is just fluff so it works in excel. Yes I know the code can be improved in a lot of ways but it works for its purpose.
Heat Penalties
Spoiler
This section is peripheral to the main argument. Enough people have been talking about TT penalties that I thought I should add it in here.
Both the linear and exponential models would benefit from more advanced penalties for running hot, though they would have to be scaled very differently.
Based on the example given by Praetor Knight, I have come up with a heat penalty scale that I believe would integrate well with exponential heat decay.
Again, this is all speculation and none of it is necessary for the implementation of the exponential model. We would really need to try it out to see how it should be adjusted.

Since a mech in TT can gain and bleed heat equal to its effective heat sinks in a single turn without any penalties, I decided that a mech using this scale should be able to reach an arbitrary heat level (I picked 60%) before the penalties start. Really it is more like 65% but regardless it seemed like a good place to start. Critical penalties (damage, ammo explosion) would be rolled once every 0.75 seconds, allowing time for mechwarriors to manually shut down their mech, flush coolant, or let the mech cool naturally.
A shutdown timer would appear when your mech is in danger of damaging itself. If this is overridden, a second timer will appear at 100 percent in which case the mech would shut down before it can take damage over 100% heat.
Any mech being over 100% heat would have to take severe amounts of damage, maybe 5% of max health per second per component?
To allow mechs to cool and to prevent extreme flamer trolling and deaths, a shutdown mech could cool 1.5x or 2x as fast. [[Although if the heat sinks are heat exchangers, wouldn't they not be on anymore? Oh well. Balance is certainly more important here.]]
All of this can be adjusted and is open to speculation as it does not directly affect the exponential model (or need thereof). We would really have to test the model first hand to be able to say what is necessary.
This section is peripheral to the main argument. Enough people have been talking about TT penalties that I thought I should add it in here.
Both the linear and exponential models would benefit from more advanced penalties for running hot, though they would have to be scaled very differently.
Based on the example given by Praetor Knight, I have come up with a heat penalty scale that I believe would integrate well with exponential heat decay.
Again, this is all speculation and none of it is necessary for the implementation of the exponential model. We would really need to try it out to see how it should be adjusted.

Since a mech in TT can gain and bleed heat equal to its effective heat sinks in a single turn without any penalties, I decided that a mech using this scale should be able to reach an arbitrary heat level (I picked 60%) before the penalties start. Really it is more like 65% but regardless it seemed like a good place to start. Critical penalties (damage, ammo explosion) would be rolled once every 0.75 seconds, allowing time for mechwarriors to manually shut down their mech, flush coolant, or let the mech cool naturally.
A shutdown timer would appear when your mech is in danger of damaging itself. If this is overridden, a second timer will appear at 100 percent in which case the mech would shut down before it can take damage over 100% heat.
Any mech being over 100% heat would have to take severe amounts of damage, maybe 5% of max health per second per component?
To allow mechs to cool and to prevent extreme flamer trolling and deaths, a shutdown mech could cool 1.5x or 2x as fast. [[Although if the heat sinks are heat exchangers, wouldn't they not be on anymore? Oh well. Balance is certainly more important here.]]
All of this can be adjusted and is open to speculation as it does not directly affect the exponential model (or need thereof). We would really have to test the model first hand to be able to say what is necessary.
I hope this is error-free. I will do my best to correct any mistakes I have made as soon as I can.
I am going away this weekend so I will answer any questions when I return.
Thank you for reading.
Edited by Ancient Demise, 14 October 2014 - 01:11 PM.

































